Introduction
Each residual macroblock is transformed, quantized and coded. Previous standards such as MPEG-1, MPEG-2, MPEG-4 and H.263 made use of the 8x8 Discrete Cosine Transform (DCT) as the basic transform. The “baseline” profile of H.264 uses three transforms depending on the type of residual data that is to be coded: a transform for the 4x4 array of luma DC coefficients in intra macroblocks (predicted in 16x16 mode), a transform for the 2x2 array of chroma DC coefficients (in any macroblock) and a transform for all other 4x4 blocks in the residual data. If the optional “adaptive block size transform” mode is used, further transforms are chosen depending on the motion compensation block size (4x8, 8x4, 8x8, 16x8, etc).
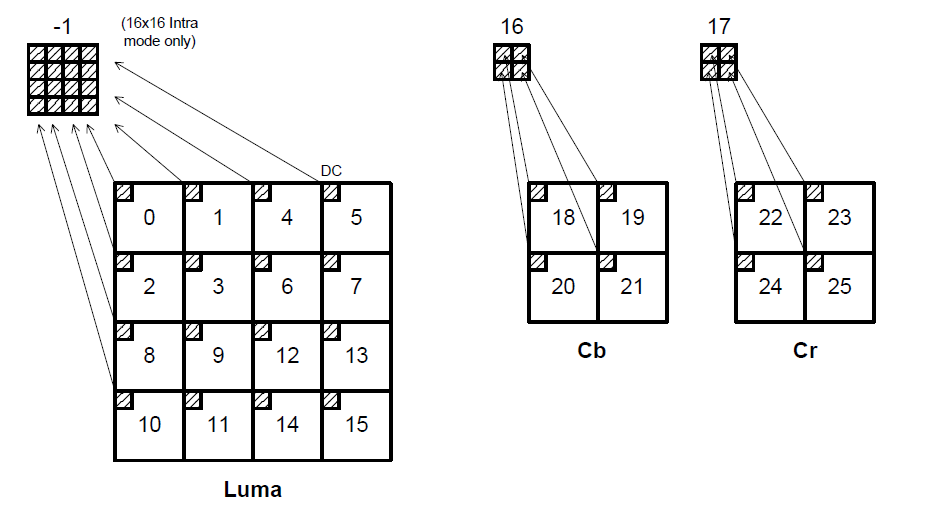
Coefficient Scan Order
The DC for 16x16, the other AC and chroma's DC AC coefficients scane order:
4x4 DCT & IDCT
The 2-D DCT could be represented as
\(Y=AXA^T\)
which could be transformed as:
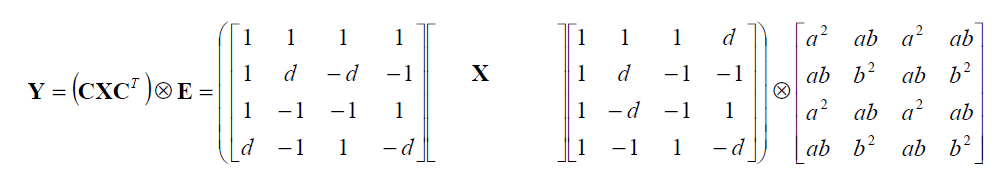
Thus DCT could be represented as:
\(Y=CXC^T \bigotimes E\)
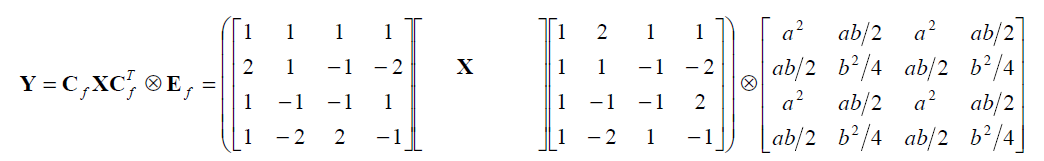
The IDCT could be represented as:
\(X^{\prime}=C^T(Y \bigotimes E)C\)

The H264 DCT only perform the \(CXC^T\) part, leave the \(\bigotimes E\) be deal with in Quant and Dequant stage.
Quantization
Quantization, in mathematics and digital signal processing, is the process of mapping input values from a large set (often a continuous set) to output values in a (countable) smaller set. Rounding and truncation are typical examples of quantization processes. Quantization is involved to some degree in nearly all digital signal processing, as the process of representing a signal in digital form ordinarily involves rounding. Quantization also forms the core of essentially all lossy compression algorithms.
The difference between an input value and its quantized value (such as round-off error) is referred to as quantization error. A device or algorithmic function that performs quantization is called a quantizer. An analog-to-digital converter is an example of a quantizer.
Quantization is a very important step in data compression. For H264:
\(Z = round(Y/Q_{step})\)
Y is coefficients of the transform described above, Z is the quantized coefficient. H264 provided 52 values of Qstep, which are indexed by a Quantization Index, QP. Qstep increase by 12.5% for increment of 1 in QP and Qstep doubles in size for every increment of 6 in QP. QP chroma is derived from QP y so QP chroma is less than QP y for value of QP y above 30.

Assume \(W=CXC^T\), then \(Z_{ij} = round(W_{ij} \frac{PF}{Q_{step}})\) The PF is the value of matrix \(E\), whose value depending on the position \((i,j)\)
To simplify the calculation, and enlarge the dynamic range, let's assume \(\frac{MF}{2^{qbits}}=\frac{PF}{Qstep}\) where \(qbits=15+floor(QP/6)\) Then:
\(Z_{ij} = round(W_{ij} \frac{MF}{2^{qbits}}) = (W_{ij}MF + f)>>qbits\)
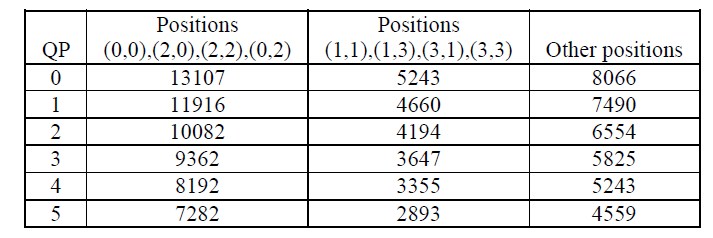
The MF is pre-calculated table as followed. For QP>5, the factores MF remain unchaged but the divisor \(2^{qbits}\) increased by a factor of 2 for each increment of 6 in QP.
Dequantization
According to previous chapter, the process of inverse transform is \(X^{\prime}=C^T(Y \bigotimes E)C\). Then the inverse quantization is:
\(X^{\prime}_{ij}=Z_{ij}*Qstep*PF*64\)
Let \(V=Qstep * PF *64\), which is also defined as pre-calculated table for \(0 \leq QP \leq 5\)
\(W^{\prime}_{ij} = Z_{ij}*V_{ij}*2^{floor(QP/6)}\)
The table of V:
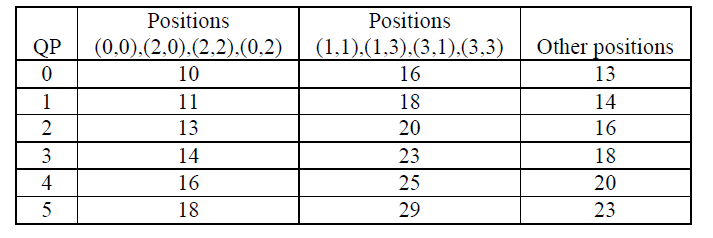
4x4 luma DC coefficient transform and quantization (16x16 Intra-mode only)
If the macroblock is encoded in 16x16 Intra prediction mode (where the entire 16x16 luminance component is predicted from neighbouring pixels), each 4x4 residual block is first transformed using the “core” transform described above \(C_{f}XC^{T}_{f}\). The DC coefficient of each 4x4 block is then transformed again using a 4x4 Hadamard transform:
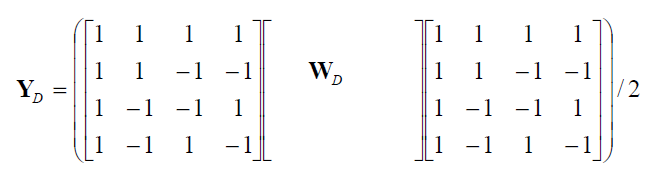
\(W_D\) is the block of 4x4 DC coefficients. The output coefficients \(Y_{D}\) are divided by 2 (with rounding). Then the \(Y_D\) are quantized:
\(Z_{D(ij)}=(Y_{D(ij)} \bullet MF_{(0,0)} + 2f) >> (qbits+1)\)
When decoding, the inverse Hadamard transform is applied followed by rescaling (not reversed as might be expected). That is [4x4DCT->4x4DC Hadamard->DC quantization->4x4DC inverse Hadamard->DC dequantization]:
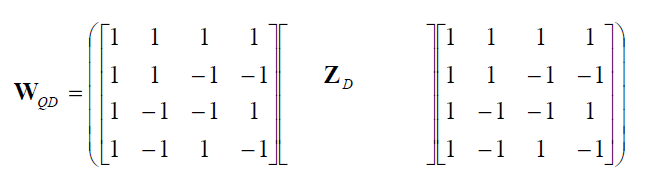
If \(QP \geq 12\), dequantization is performed by:
\(W_D = W_{QD} \bullet V_{(0,0)} \bullet 2^{floor(QP/6)-2}\)
if \(QP < 12\), dequantization is performed by:
\(W_D = (W_{QD} \bullet V_{(0,0)}+2^{1-floor(QP/6))}>>(2-floor(QP/6))\)
2x2 chroma DC coefficient transform and quantization
The DC of chroma have the same operation of chroma. 2x2 Transform:
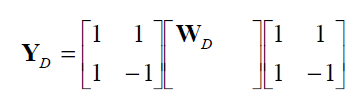
The Quantization of the 2x2 output if performed by:
\(Z_{D} = Y_{D(ij)} \bullet MF_{(0,0)}+2f)>>(qbits+1)\)
during decoding, the inverse transform is:
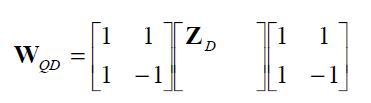
If \(QP \geq 6\), dequantization is performed by:
\(W_D = W_{QD} \bullet V_{(0,0)} \bullet 2^{floor(QP/6)-1}\)
if \(QP < 6\), dequantization is performed by:
\(W_D = (W_{QD} \bullet V_{(0,0)})>>1\)
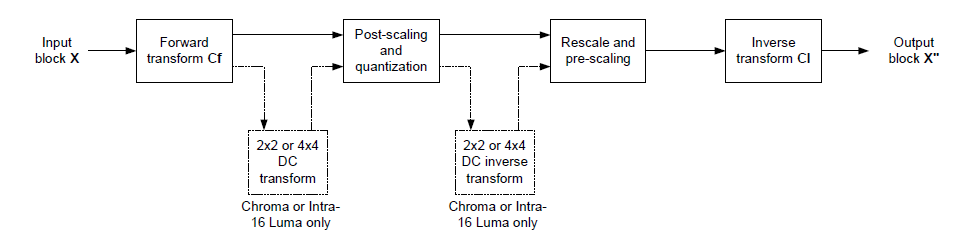
Transform & QDQ Flow
Comments